Defines a surface of revolution. More...

#include <cadex/Geom/SurfaceOfRevolution.hxx>

Inheritance diagram for cadex::Geom::SurfaceOfRevolution:

Public Member Functions
	SurfaceOfRevolution ()
	Constructor.

	SurfaceOfRevolution (const Geom::Curve &theBasisCurve, const Geom::Point &theLocation, const Geom::Direction &theDirection)
	Constructor.

Geom::Point	Location () const
	Returns an origin point of a rotation axis.

Public Member Functions inherited from cadex::Geom::SweptSurface
	SweptSurface ()
	Constructor.

Geom::Curve	BasisCurve () const

Geom::Direction	Direction () const

Public Member Functions inherited from cadex::Geom::Surface
	Surface ()
	Constructor.

SurfaceType	Type () const
	Returns a surface type.

Geom::Continuity	Continuity () const
	Returns a continuity type of the surface.

Point	Value (double theParameterU, double theParameterV) const
	Evaluates a point on the surface.

Direction	Normal (double theParameterU, double theParameterV) const
	Returns the normal direction theNormal at the current point.

bool	IsUPeriodic () const
	Returns true if the surface is periodic in U direction.

bool	IsVPeriodic () const
	Returns true if the surface is periodic in V direction.

double	UMin () const
	Returns a minimum parameter of a definition domain in U direction.

double	UMax () const
	Returns a maximum parameter of a definition domain in U direction.

double	VMin () const
	Returns a minimum parameter of a definition domain in V direction.

double	VMax () const
	Returns a maximum parameter of a definition domain in V direction.

void	Domain (double &theUMin, double &theUMax, double &theVMin, double &theVMax) const
	Returns a definition domain.

bool	IsTrimmed () const
	Returns whether surface is trimmed or not.

void	SetTrim (double theUFirst, double theULast, double theVFirst, double theVLast)
	Trims surface with [theUFirst, theULast] x [theVFirst, theVLast] section.

void	Transform (const Transformation &theTransformation)
	Applies transformation matrix to this object.

Surface	Transformed (const Transformation &theTransformation) const
	Returns a copy this object after applying transformation.

void	D0 (double theParameterU, double theParameterV, Point &theValue) const
	Returns the point theValue of parameter theU, theV on the surface.

void	D1 (double theParameterU, double theParameterV, Point &theValue, Vector &theD1U, Vector &theD1V) const
	Returns the point theValue and the first derivatives in the directions U theD1U and V theD1V at this point.

void	D2 (double theParameterU, double theParameterV, Point &theValue, Vector &theD1U, Vector &theD1V, Vector &theD2U, Vector &theD2V, Vector &theD2UV) const
	Returns the point theValue, the first and the second derivatives in the directions U and V at this point.

bool	DN (double theParameterU, double theParameterV, size_t theDerivativeOrder, Geom::Point &theValue, std::vector< Geom::Vector > &theD) const

void	Curvature (double theParameterU, double theParameterV, Direction &thePrincipalMaxDirection, Direction &thePrincipalMinDirection) const
	Returns the max and min principal curvature directions multiplied by max and min value of curvature respectively.

void	Curvature (double theParameterU, double theParameterV, Direction &thePrincipalMaxDirection, Direction &thePrincipalMinDirection, double &theMaxCurvature, double &theMinCurvature) const
	Returns the max and min principal curvature directions and their values.

void	Mirror (const Point &thePoint)

void	Mirror (const Axis1d &theAxis)

void	Mirror (const Axis3d &theAxis)

Surface	Mirrored (const Point &theRef) const

Surface	Mirrored (const Axis1d &theAxis) const

Surface	Mirrored (const Axis3d &theAxis) const

void	Rotate (const Axis1d &theAxis, double theAngle)

Surface	Rotated (const Axis1d &theAxis, double theAngle) const

void	Translate (const Vector &theVector)

Surface	Translated (const Vector &theVector) const

void	Scale (const Point &thePoint, double theScale)

Surface	Scaled (const Point &thePoint, double theScale) const

Public Member Functions inherited from cadex::BaseObject
size_t	Id () const
	Return unique identifier of public object.

internal::BaseObjectImpl *	Impl () const

bool	IsNull () const

	operator bool () const

template<typename T >
bool	IsOfType () const

template<typename T >
T *	Impl () const
	Reserved for internal use.

Static Public Member Functions
static bool	CompareType (const BaseObject &theObject)

Static Public Member Functions inherited from cadex::Geom::SweptSurface
static bool	CompareType (const BaseObject &theObject)

Static Public Member Functions inherited from cadex::Geom::Surface
static bool	CompareType (const BaseObject &theObject)

Static Public Member Functions inherited from cadex::Geom::Geometry
static bool	CompareType (const BaseObject &theObject)

Additional Inherited Members
Public Types inherited from cadex::BaseObject
typedef std::shared_ptr< internal::BaseObjectImpl >	ImplType

Protected Member Functions inherited from cadex::Geom::SweptSurface
	SweptSurface (const ImplType &theImpl)

Protected Member Functions inherited from cadex::Geom::Surface
	Surface (const ImplType &theImpl)

Protected Member Functions inherited from cadex::Geom::Geometry
	Geometry (const ImplType &theImpl)

Protected Member Functions inherited from cadex::BaseObject
	BaseObject (const ImplType &theImpl)

Detailed Description

Defines a surface of revolution.

Surface of revolution is defined by a basis curve and a rotation axis. The following image depicts an example of a surface of revolution:

Surface of revolution

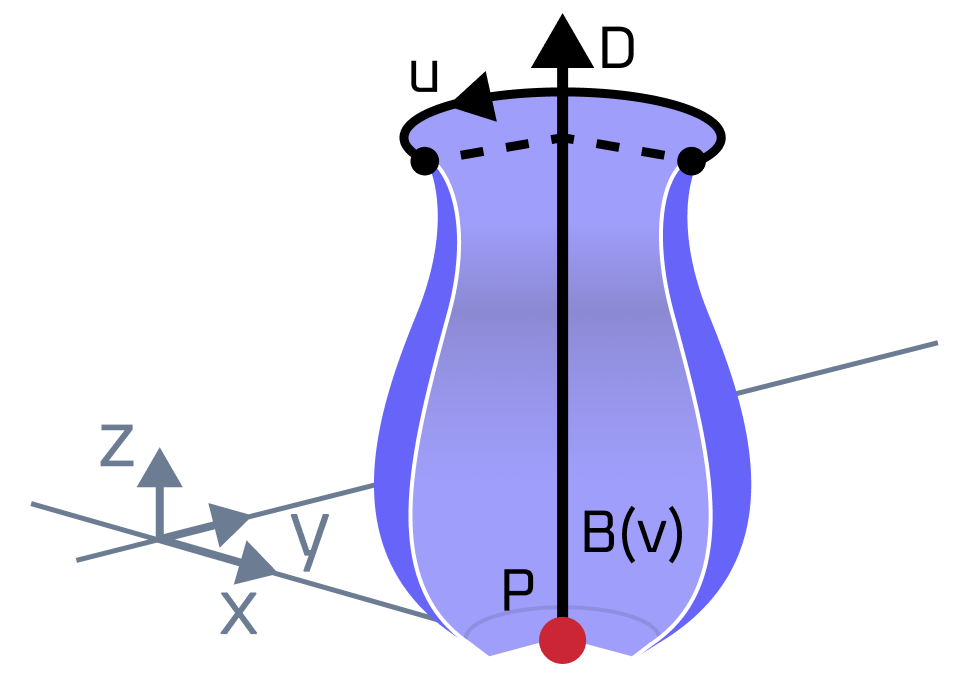
A surface of revolution is parametrized as follows: \(\mathbf{S}(u,v) = \mathbf{Z}(v) + \cos(u)(\mathbf{B}(v) - \mathbf{Z}(v)) + \mathbf{D}\times\sin(u)(\mathbf{B}(v) - \mathbf{Z}(v))\), where:

\(\mathbf{P}\) is an origin point specifying rotation axis,
\(\mathbf{D}\) is unit vector specifying rotation axis,
\(\mathbf{B}(v)\) is a basis curve,
\(\mathbf{Z}(v)\) is a projection of a point on the basis curve onto a rotation axis, \(\mathbf{Z}(v) = \mathbf{P} + ((\mathbf{B}(v) - \mathbf{P})\cdot\mathbf{D})\mathbf{D}\),
\(u\) belongs to \([0, 2\pi]\),
\(v\) belongs to a basis curve definition domain.

U-parameter is an angle of rotation around the axis counterclockwise, and V-parameter is s a parameter along the curve \(\mathbf{B}(v)\). Thus, U-isolines are correspond to curve \(\mathbf{B}(v)\) rotated around the rotation axis and V-isolines are circles perpendicular to rotation axis with radius equal to distance from the axis to a point on the basis curve at parameter V. U-isoline at \(u=0\) is the basis curve itself.

The curve \(\mathbf{B}(v)\) should be planar although this is not enforced. It should not cross the rotation axis, except possibly at the end points.

Surface or revolution is periodic along U with period \(2\pi\). It is V-periodic if the basis curve is periodic itself.

If a face lies on a full range of U its boundary wire will contain two seam-edges at parameters UMin() and UMax(). Likewise, if the surface is V-periodic the wire will contain two seam-edges at parameters VMin() and VMax(). If the basis curve has end point(s) lying on a rotation axis then the wire will contain degenerated edge(s) at respective point(s).

Constructor & Destructor Documentation

◆ SurfaceOfRevolution()

cadex::Geom::SurfaceOfRevolution::SurfaceOfRevolution	(	const Geom::Curve &	theBasisCurve,
		const Geom::Point &	theLocation,
		const Geom::Direction &	theDirection )

Constructor.

Creates a surface of revolution from a basis curve and a rotation axis.

Member Function Documentation

◆ Location()

Geom::Point cadex::Geom::SurfaceOfRevolution::Location ( ) const

Returns an origin point of a rotation axis.

Returns the value specified in the constructor.

Public Member Functions

Static Public Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

◆ SurfaceOfRevolution()

Member Function Documentation

◆ Location()